Purely mathematical perspective on delaying the second dose of the SARS-CoV-2 vaccine

By Michael Greenwood, M.Sc.Feb 17 2021

The three most popularly administered severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) vaccines developed so far (Pfizer, Oxford/AstraZeneca, and Moderna) recommend that a person receive two doses of the vaccine spaced a number of weeks apart in order to achieve maximum efficacy. However, high demand for the vaccines has raised questions as to whether it would be better in the long term to ensure that as much of the population as possible has received the first dose, i.e., vaccinate twice as many people with a lower rate of efficacy.

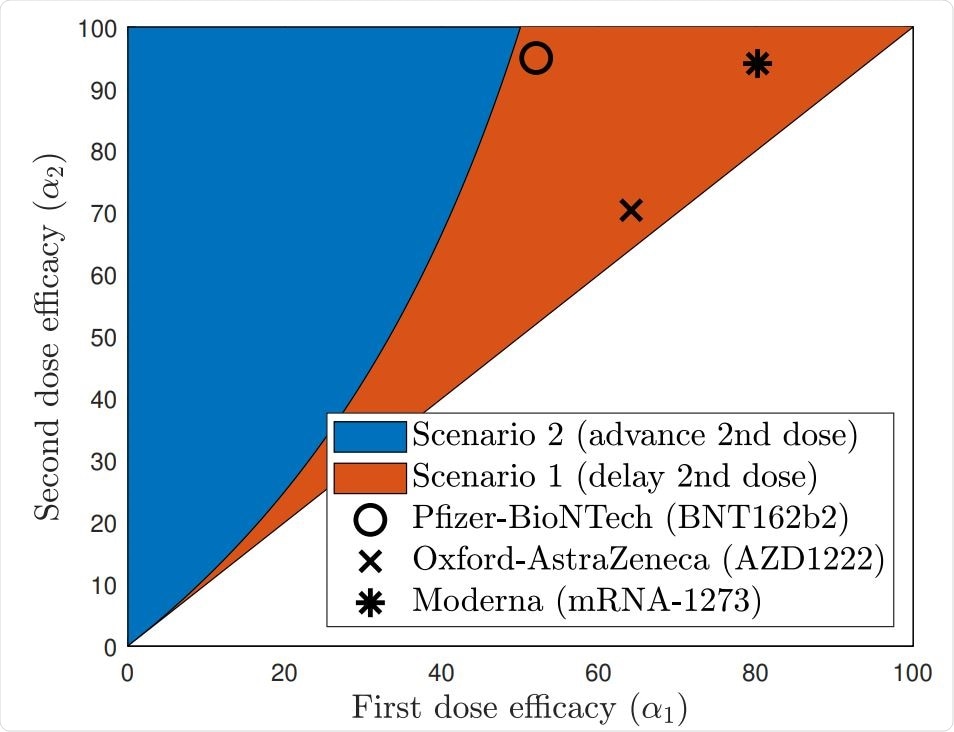
The answer to the question of delaying or advancing the second COVID-19 vaccine dose depends on the efficacies of each of the first and the second doses. This figure depicts the region (in red) where the best scenario would be to delay the second dose and the region (in blue) where the second dose should be advanced for optimal outcomes.

This news article was a review of a preliminary scientific report that had not undergone peer-review at the time of publication. Since its initial publication, the scientific report has now been peer reviewed and accepted for publication in a Scientific Journal. Links to the preliminary and peer-reviewed reports are available in the Sources section at the bottom of this article. View Sources

A Canadian research paper recently uploaded to the preprint server medRxiv* (17^th Feb 2021) by Soulaimane Berkane et al. aims to mathematically establish the optimal course of action in terms of most efficiently distributing the vaccine and achieving the best possible level of immunization.

The paper is based on a comparison in vaccine efficacy from the first to the second dose, assuming that all of the population will eventually receive both doses. The two extremes considered by the authors, therefore, are the application of both doses as soon as is possible and clinically recommended, and the application of the second dose at the latest possible clinically relevant point.

A simple equation was developed based on the idea that the second dose will always be more effective than the first alone, and requires only the efficacy of each dose to be entered:

Where x₁ and x₂ denote the efficacy of the first and second doses as a percentage, respectively.

The immediate result of formula 1 indicates that if the first dose's efficacy is above 50%, it will be more effective to delay the second dose's administration for as long as possible, regardless of how efficacious the second dose is. Interestingly, the equation implies that even in cases where the first dose is shown to have less than 50% efficacy this may still be the optimum strategy, as the efficacy of the second dose must exceed the threshold implied. For example, if x₁ = 25%, then inputting the values into equation 2 gives 33.34%. Therefore, the second dose should only be given as quickly as possible if it is more efficacious.

The Pfizer, Oxford/AstraZeneca, and Moderna vaccines have each claimed more than 50% efficacy from the first dose and over 90% from the second, suggesting that delayed vaccination may be the best strategy.

Further, the daily rate of vaccination in the population was considered, and another simple formula drafted to determine the maximized total daily number of people that are effectively inoculated:

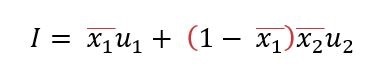
Where 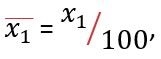, to put the percentage into the form of a proportion, and u₁ is the number vaccinated with the first dose per day. Thus, x₁u₁ represents the daily effectively vaccinated population. The latter terms of the equation refer to the portion of the population that has received both the first and second doses of the vaccine.

Since u₁ represents the total daily vaccination rate, and u₂ represents the daily total receiving the second dose, u_{1 +} u_{2 =} u, the total daily overall dose. This allowed the authors to rewrite the equation as:

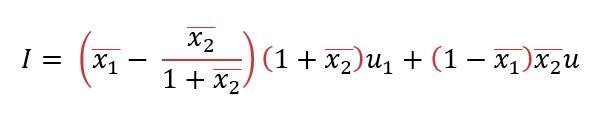
According to this equation, the optimal vaccination strategy depends on the first term of the equation. If the sign of the first term is positive, then the second dose should be delayed, otherwise, the doses should be given as close together as possible.

For example, if the first dose of the vaccine is 50% effective, while the second is 75% effective, then the result of the first term is +0.07, indicating an optimal delayed strategy. In this case, then u₁ can be set to 1 (u), meaning that every vaccine being given is the first dose to somebody.

Given current evidence and the ideas presented in this work, it may be optimal to delay second doses for as long as possible, depending on vaccine availability and population compliance.

This news article was a review of a preliminary scientific report that had not undergone peer-review at the time of publication. Since its initial publication, the scientific report has now been peer reviewed and accepted for publication in a Scientific Journal. Links to the preliminary and peer-reviewed reports are available in the Sources section at the bottom of this article. View Sources